Registral Streams, Fusion, and Prolongation in Åke Hermanson’s Alarme for Solo Horn, Op. 1

Stephen Harper

1. Introduction

The topic of prolongation in atonal music has been one that has fascinated analysts almost from the instant that Heinrich Schenker’s work on tonal music became widely known. Among these early writers, Allen Forte, Roy Travis, Adele Katz, and Felix Salzerpresented reductive voice-leading graphs of atonal works to demonstrate the power of prolongational explanation in the atonal repertoire.[1] However, there continued to be a gnawing sense that something was seriously wrong here, that perhaps the concept of prolongation was not truly applicable to atonal music. Beginning in the late 1980s, Joseph N. Straus and Fred Lerdahl each produced extended and insightful arguments, across a series of essays, on the validity of the concept of prolongation for this repertoire. In 1987, Straus articulated the argument against prolongation in his essay “The Problem of Prolongation in Post-Tonal Music.” His article served two important functions. First, he articulated a series of four conditions for prolongation, of which the post-tonal repertoire (in his view) exhibited none.[2] He then clearly differentiated prolongation from association, asserting that, while much of what has passed for prolongational analysis in post-tonal music was really associational, these associations might still be analytically salient.

A counterargument was offered by Fred Lerdahl, first in “Atonal Prolongational Structures” (1989), then in “Issues in Prolongational Theory: A Response to Larson” (1997). Lerdahl’s view was that Straus’s conditions characterized tonal prolongation, but did not, thereby, exhaust the field. More specifically, the main difference between tonal and atonal music is that the latter does not have stability conditions (addressed in Straus’s first two conditions); however, atonal music still “project[s] the relative salience of events. … [A]tonal music [thus] collapses the distinction between salience and structural importance” (1989, 73). Much of Lerdahl’s analytic apparatus comes directly from his book with Ray Jackendoff on tonal music, A Generative Theory of Tonal Music (1983, henceforth GTTM), reinforcing his point that fundamental cognitive procedures must underly our processing of both these types of music.

Olli Väisälä has produced the most comprehensive assessment of the theoretical foundation for atonal prolongation in his Prolongation in Early Post-Tonal Music (2004). Väisälä roots his discussion in psychoacoustics and a reconsideration of intervals to argue in favor of prolongational workings in a certain collection of pieces. The reworking of interval theory is crucial to avoiding some of the problems pointed out by Straus.

But, despite Lerdahl and Väisälä, there are still some rather foundational difficulties in asserting a prolongational analysis in a post-tonal setting. One of these is discerning what Väisälä calls the referential harmony (1). In tonal music, the “Chord of Nature” is the referential harmony for the entire repertoire; obviously, nothing analogous can be asserted about the atonal repertoire. Even finding the contextually-determined referential harmony for a single piece is hard enough. Väisälä, in his section 6.1.1 and in a footnote offers these words: “I will not attempt to describe a generally applicable strategy for tracing the referential harmony, but only make some observations of where the clearest clues to the referential harmony can be found in the present examples” (89). Väisälä’s footnote attached to this sentence reads: “These observations do not purport to describe my actual processes of tracing the referential harmony. Such processes are more complex than can be described in this way; moreover, they have largely fallen from memory.”[3]

Second, classical tonality has a well-developed concept of “voice” that (among other things) codifies how voices move in certain situations; no such general notion exists in atonal music. As Väisälä points out, “voice” is an astonishingly complex notion that goes far beyond stream segregation (the more or less automatic separation of musical lines, as, for example, in compound melodies); in his words, voice “involves extensive cognitive generalizations and extensions, concerning the dimensions of both pitch and time” (87).

In this essay, I will examine Åke Hermanson’s Alarme for solo horn, with an eye toward harmonic progression and prolongation. In particular, I will examine how harmonies might be fused from registrally distinct musical streams, explicitly relating fusion to motivic substance in a way that may prove fruitful across a larger span of atonal pieces. I also examine how registral streams might constitute a concept of “voice” for the atonal repertoire. Again, although Väisälä specifically cautions against simply equating stream and voice, using registral streams as a basis for voice (as enriched and reinforced by harmonic change) may help mitigate some unmotivated tonal intrusions into prolongational analyses of atonal works.[4] Additionally, as a prerequisite for using registral streams as voices, I explore the possibility of register-space (r-space). In r-space, the pitch spectrum is divided into a series of malleably-bounded regions. We can then trace musical lines within these regions.

2. Preliminaries

2.1 R-Space

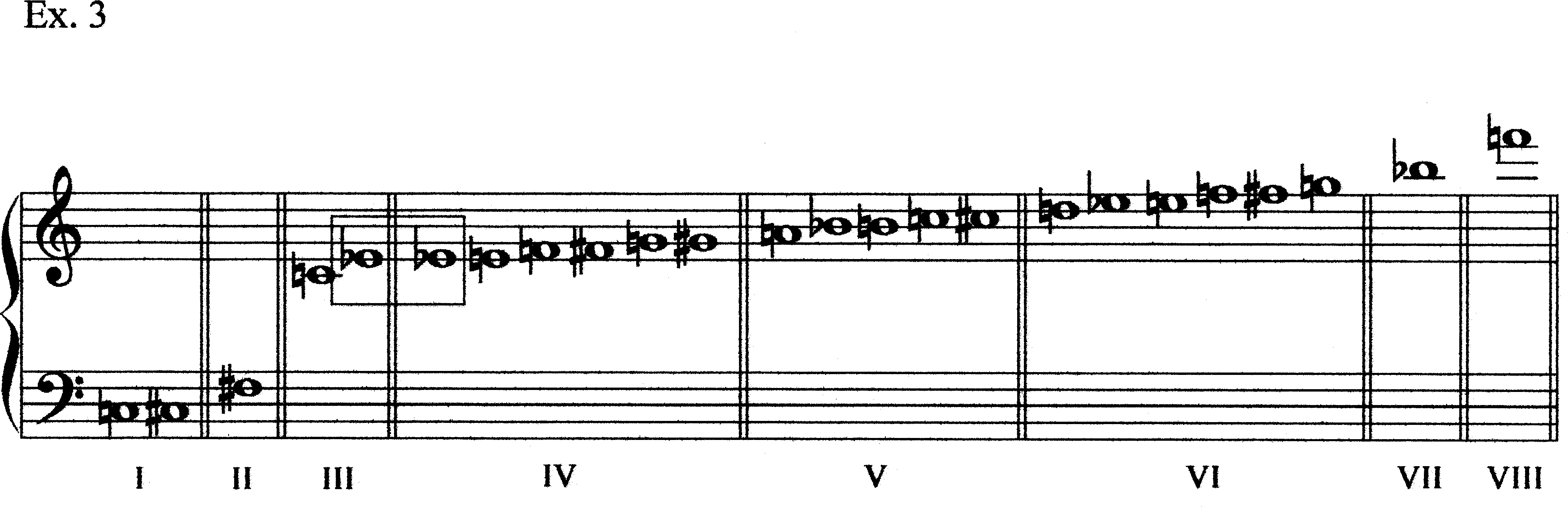
Example 1 shows the pitches of mm. 1.3–7.2 of Alarme. These pitches represent three distinct registers, low-to-high spatial regions of activity. In Alarme, there are a total of eight registers that are activated during the piece; Example 2 shows a protoypical representative of each of these registers (the registers are numbered with Roman numerals). [Throughout this paper, I refer to the written pitches rather than the sounding pitches, with the following exception: Hermanson follows the old tradition of having the horn (in F) when notated in the bass clef sound a P4 higher (rather than a P5 lower) than written; throughout, I have rendered his bass-clef notes an octave higher for consistency’s sake.] Some of these registers are represented by only one pitch (indeed, some by only one note) in the work, while in other registers several different pitches are employed. Example 3 gives the entire pitch-content of Alarme and the registral boundaries. Note that Eb4 is used sometimes as a representative of Register III and sometimes as a representative of Register IV. This example leaves many unanswered questions about registral boundaries. Two points should be made here. First, the boundaries of r-space regions are malleable; it is quite possible that one pitch could belong to different registers at different points in the piece. Indeed, it is actually a unique property of this piece that there is so little overlapping of regions. Second, the analysis itself will help clarify how registers are separated (right now it is by no means obvious how these boundaries were determined). R-sets are collections of register-identification numbers (Arabic numbers are more useful than Roman numerals here); they can be transposed so that the first element is “0” for comparison purposes (Ex. 4).

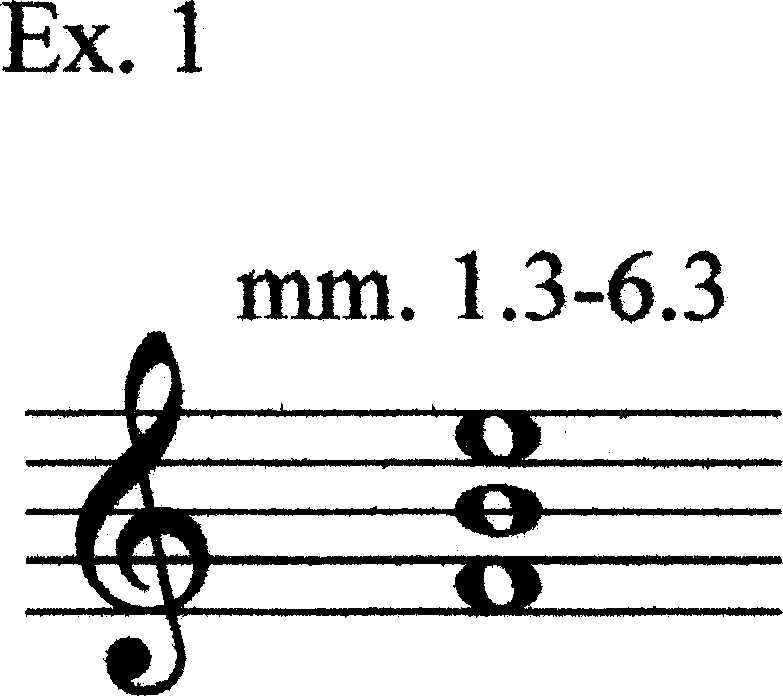
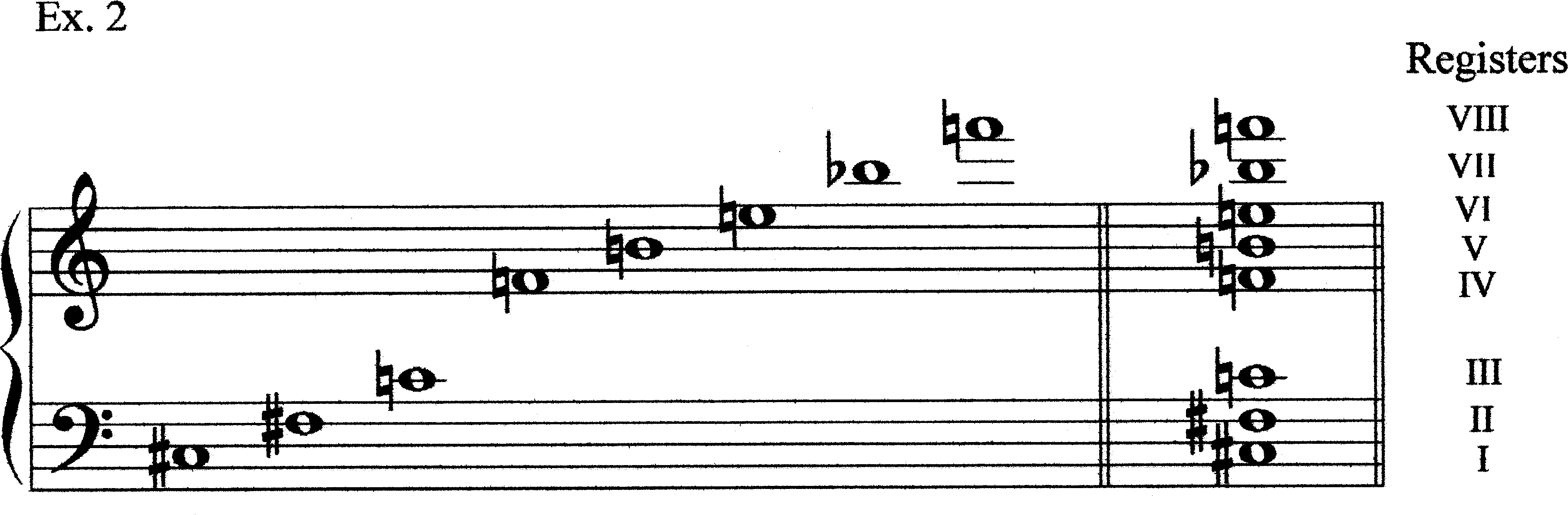
This piece-specific model of r-space provides the distinctions between registral streams/lines. Where two notes belong to different regions of r-space, they are generally assumed to belong to different “voices;” these voices can then be fused into harmonies.

2.2 Assembling Harmonies through Fusion

A concise work for solo instrument like Alarme makes for an interesting study in atonal prolongation. Since the horn is not asked to play any multiphonics in the piece, all of the “harmonies” of the work must be assembled by the listener. This can be done by hypothesizing an arpeggiation and/or through fusion. Fusion is the process by which events that are not literally simultaneous appear to imply a simultaneity. The prototypical example is an Alberti bass pattern, which (in reduction) implies a stacked chord of multiple voices.

Fusion is obviously related to registral streaming. Lerdahl and Jackendoff explicitly note the relationship in GTTM: “Fusion in time-span reduction corresponds to the perceptual phenomenon of “auditory stream segregation,’ where one hears two voices instead of a single oscillating one (Bregman and Campbell 1971).” Väisälä points out that there is research to indicate that two alternating pitches will be more or less automatically heard as “forming separate streams unless their distance goes under three or four semitones (depending somewhat on their temporal rate)” (87).[5]

Fusion as discussed by Lerdahl and Jackendoff is a relatively local phenomenon. The issue specifically arises in the selection of a “head” for a time span;[6] the general principle that a single event is the head of a time-span is “relaxed” to allow for a fused event to serve as the head. Again, using an Alberti bass as an example, the entire chord implied by the figuration can be the head of a span. Lerdahl and Jackendoff suggest as a temporal boundary for fusion the principle that events from different groups (or time-spans) are not candidates for fusion; instead, where such events belong to the same harmony, they are said to constitute an arpeggiation.

However, in “Atonal Prolongational Structures,” Lerdahl seems to take a more expansive view of fusion. Additionally, he argues that fusion is even more important in atonal works than in tonal ones. He writes, “Fusion seems to be needed more often for atonal than for tonal music, which … lacks the harmonic and voice-leading constraints of tonal music. In atonal music it is far easier to hear a succession of widely-spaced pitches as an arpeggiation. This is one reason why so much contemporary music sounds static” (1989, 79).

2.3 Registral Streaming, Voice Leading, And Prolongation

Once harmonies are assembled, we can then see how they move. Harmonic motion will inevitably involve displacement; a chord-tone in one harmony is replaced by a different chord-tone in the new harmony (indeed, the displacement signals the change of harmony). [This is true even where distinct harmonies might share one or more pitches/pitch classes; in tonal music, more often than not there is not complete displacement.] Registral streaming will form a basis for voice identification; voice leading will provide clues concerning prolongational areas. Streaming and voice leading, of course, are intimately tied to the motivic surface of the music; the motives themselves help articulate the streams.

2.4 Motive Categories in Alarme

There are three main categories of motives in Alarme: 1) oscillating motives; 2) steady-state motives; and 3) “special” motives. Oscillating motives are those in which the musical line goes back and forth between two pitches. To obviously “count” as an oscillating motive, the passage must have at least four notes involving two pitches and the contour <0101> or <1010>. The first oscillating motive in Alarme is in mm. 1.3–3.2 (Ex. 5). There are seven notes, all of equal value, and the line alternates between E5 and B4. This motive is a fairly obvious siren icon. The oscillation implies two distinct streams, and, thus, two registers. In part, this is simply because the pitches are relatively far apart. The oscillating motives will be the most helpful and least controversial materials for assembling harmonies in Alarme.

All sounding examples come from “Åke Hermanson Alarme” (Caprice CAP 22056), performed by Ib Lanzky-Otto, used by kind permission from Caprice Records.

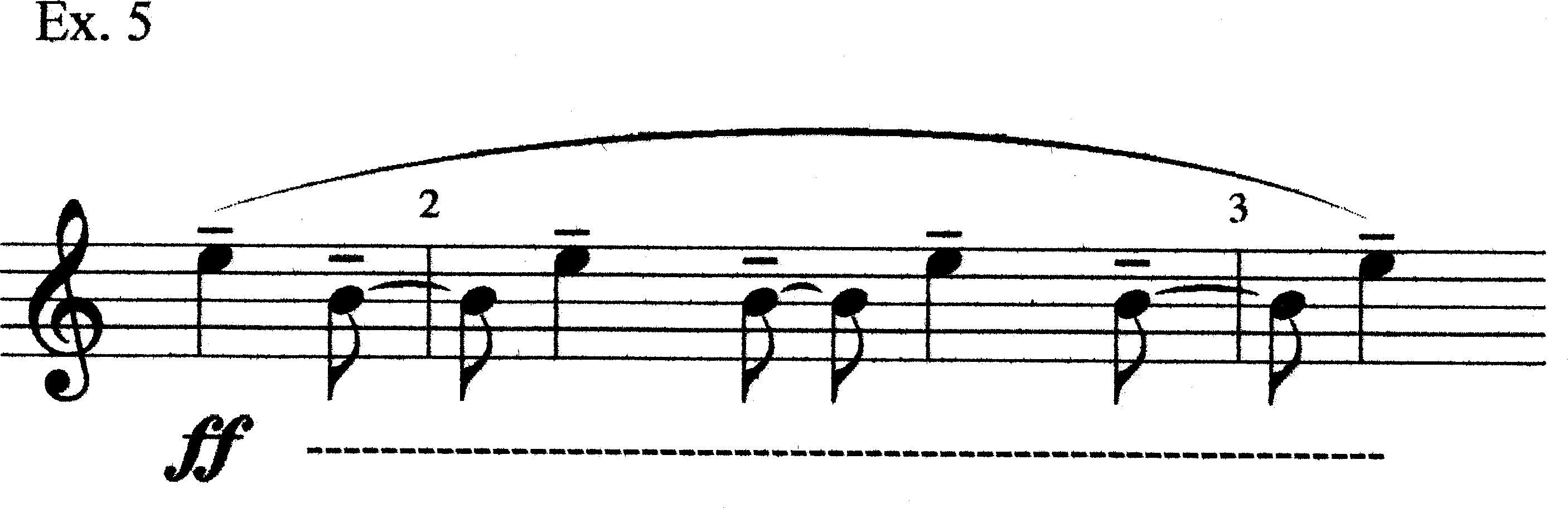
Steady-state motives involve a single pitch. These are prototypically motivic where there are consecutive unembellished statements of a single pitch; an example is given in Ex. 6 (mm. 3.3–6.3). Obviously, steady-state motives present the harmonic pitch in the specific register that is operative throughout the passage. As “fragments” of steady-state motives we have singletons, single notes presented in isolation; these are often part of an arpeggiation. Example 7 shows one such area (mm. 28–30.3). Arpeggiations are, necessarily, presentations of a harmony (or portion of a harmony), but the harmonic boundaries in arpeggiated passages may spark controversy where pitches are not obviously displaced within an r-space region.

Some steady-state motives are presented with embellishments. At first we will take note of those with M2 lower neighboring tones (either as grace notes or in a dotted eighth-sixteenth rhythm; Ex. 8 illustrates). These motive statements are not considered oscillations; the M2 is the prototypical within-voice motion for this piece. In reduction, these are rather straightforward, with a clear distinction between embellished and embellishing pitches.

There are also some passages that mix the oscillating and steady-state types. These include embellished steady-state motives where the grace note is a tritone away from the embellished note. Although these are basically either steady-state ideas or singleton statements that are part of an arpeggiation, the tritone grace notes engage another register, and, thus, another stream. The figures often help establish or clarify a harmony that governs a longer passage. One such example (mm. 18.2–18.4)is given as Ex. 9. These segments are reduced like oscillations; the two registers are represented as a simultaneity.

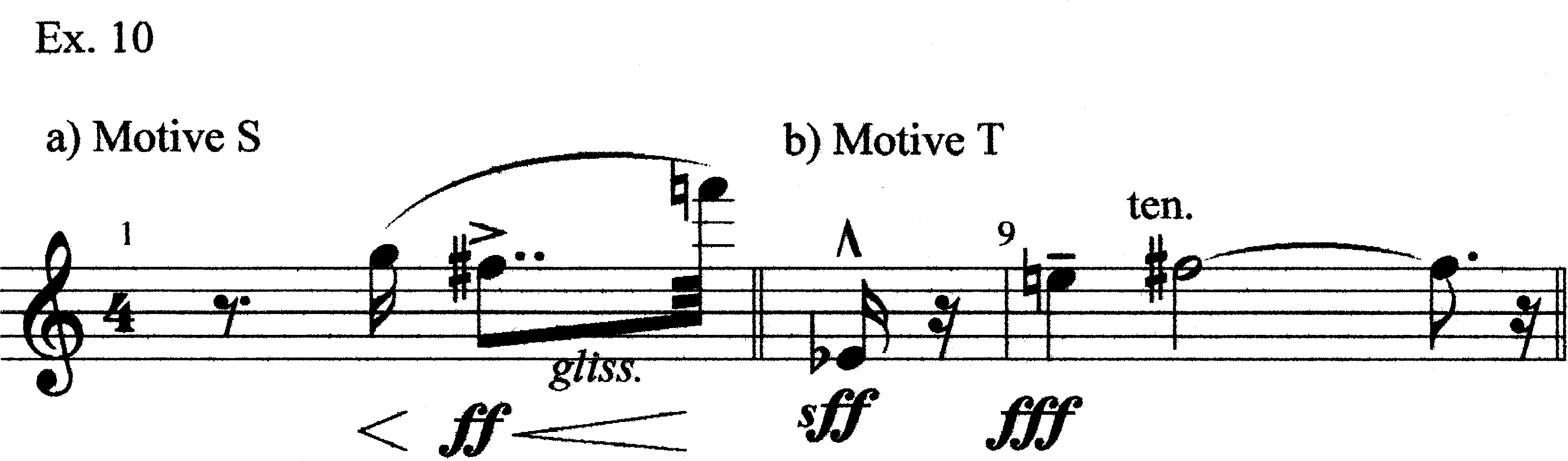
Finally, there are the “special” motives, motives that are not just abstract gesture-types, but characteristic, piece-specific ideas. The two significant such motives in Alarme are seen in Ex. 10. The reductions for these motives will be explained below. To begin our analysis, we will examine mm. 1–9 in detail.

3. Analysis of Alarme

3.1 Trip through the Piece

a. Measures 1–9

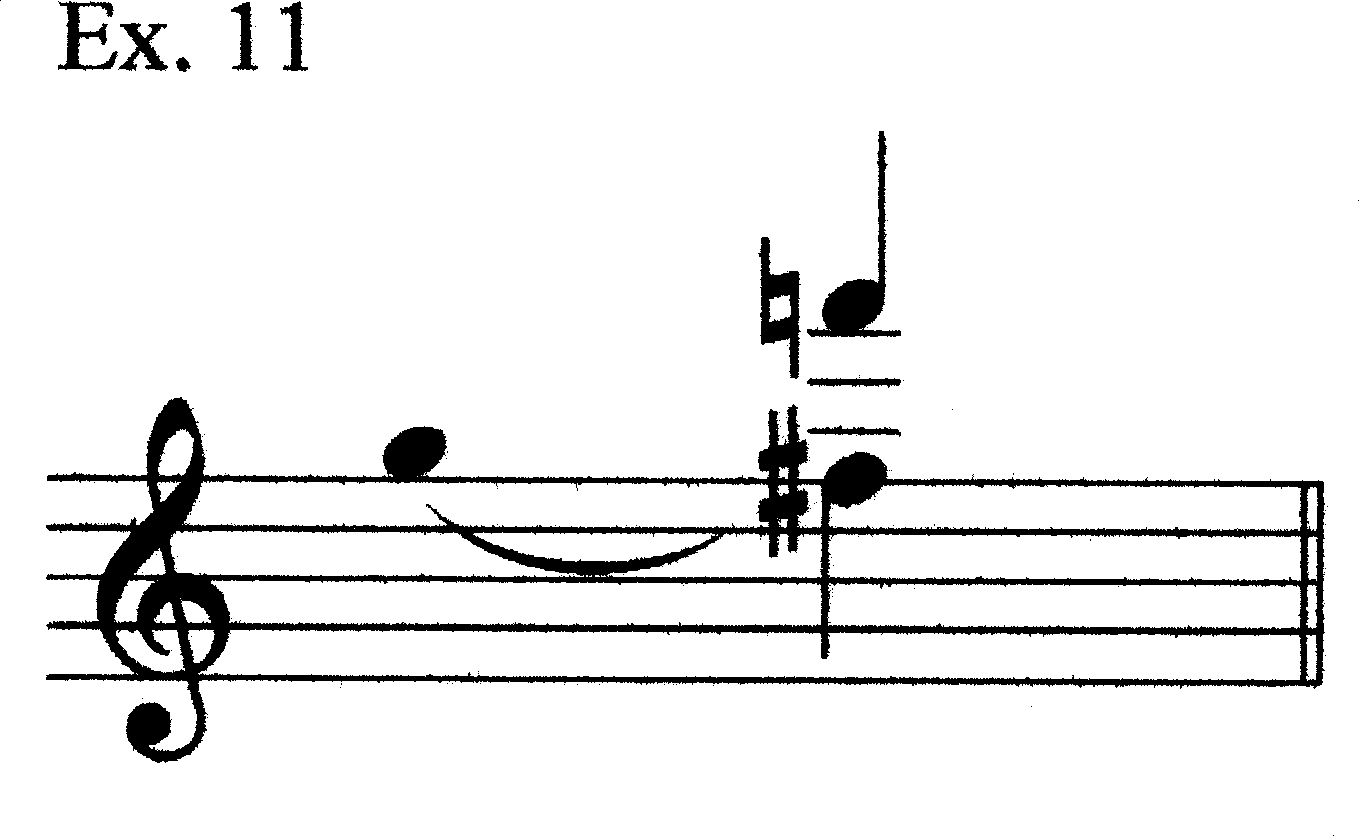
The piece begins with an iconic “scream,” Motive S. This motive invokes two registers, VI and VIII. [It should be pointed out that this is the only time Register VIII is invoked in the piece.] Of the three notes, F#5 gets an agogic and dynamic accent, whereas F6 gets a tonal accent. Even the G5, though, is special by virtue of its coming first. The F#5 and F6 can reasonably be seen as a harmonic entity; this intuition will be “confirmed” elsewhere in the piece through Hermanson’s frequent use of int. 11 within sonorities. This gesture is a curtain-raising one; it grabs the listener’s attention, but is essentially prologue to what follows. Example 11 reduces the gesture.

In mm. 1.3 through 7.2 we have two iconic sirens, one oscillating between E5 and B4, the other being a steady-state (but crescendoing) siren on F4. The E5 and B4 are taken as representing two strands (VI and V, respectively), and I think it is relatively uncontroversial to invoke the implied simultaneity. It is less obvious, however, why F4 should be added to the oscillating dyad to make a reference trichord sonority, Chord A (Ex. 12). The grace note B4 in m. 6 helps us make the association, however.

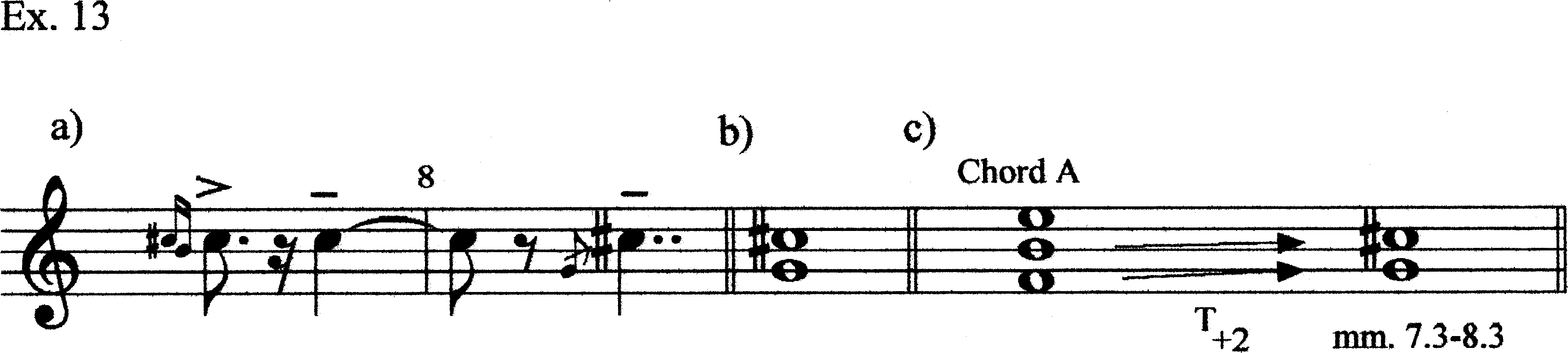
In mm. 7–8, we have an embellished steady-state motive on C#5. The grace note B4 helps us tie this C# with the previous B4. The earlier B4 has now been displaced by a C#5 in the same register (V). Further, the C#5 is then embellished in m. 8 with a grace note G4. This G4 belongs to the same register as the earlier F4 (IV). In both cases, the note from Chord A has been transposed +2 (in p-space; Ex. 13).

In mm. 8.4–9 we have another special motive, which I’ve labelled “Motive T.” The motive ends with E5 moving to F#5; F#5 displaces the E4 of Chord A. Thus, all three notes of Chord A have replaced by their +2 counterparts, making Chord B (Ex. 14).

This last motion, E5–F#5, raises a question: Has the E4 been in effect in mm. 7–8 when the other voices have been moved by +2? [The same issue applies to the motion from F4 to G4 in m. 8, but is less strikingly presented there.] While in principle this seems unanswerable at this point, later statements of the motive seem to clarify the issue somewhat. Consider, for example, the statement in mm. 45–46. By presenting the Eb4–E5 space first without the D5, Hermanson points to understanding the figure as having an embellishing incomplete neighbor within it. Since the E5 in m. 9 is not hypothesized as a note tied-over from Chord A into the Chord B time span (but, rather, an incomplete neighbor within a Chord B area), we might then make the hypothesis that E5 is implicitly displaced around the same time B4 and F4 are explicitly displaced (by C#5 and G4, respectively). Still, it has been nearly six full bars since Register VI has been engaged (approximately 19 seconds at this tempo). Rather than asserting that F#5 displaces E5, it can be argued that time displaces E5 and F#5 is a more or less unassociated new beginning for Register VI.[7]

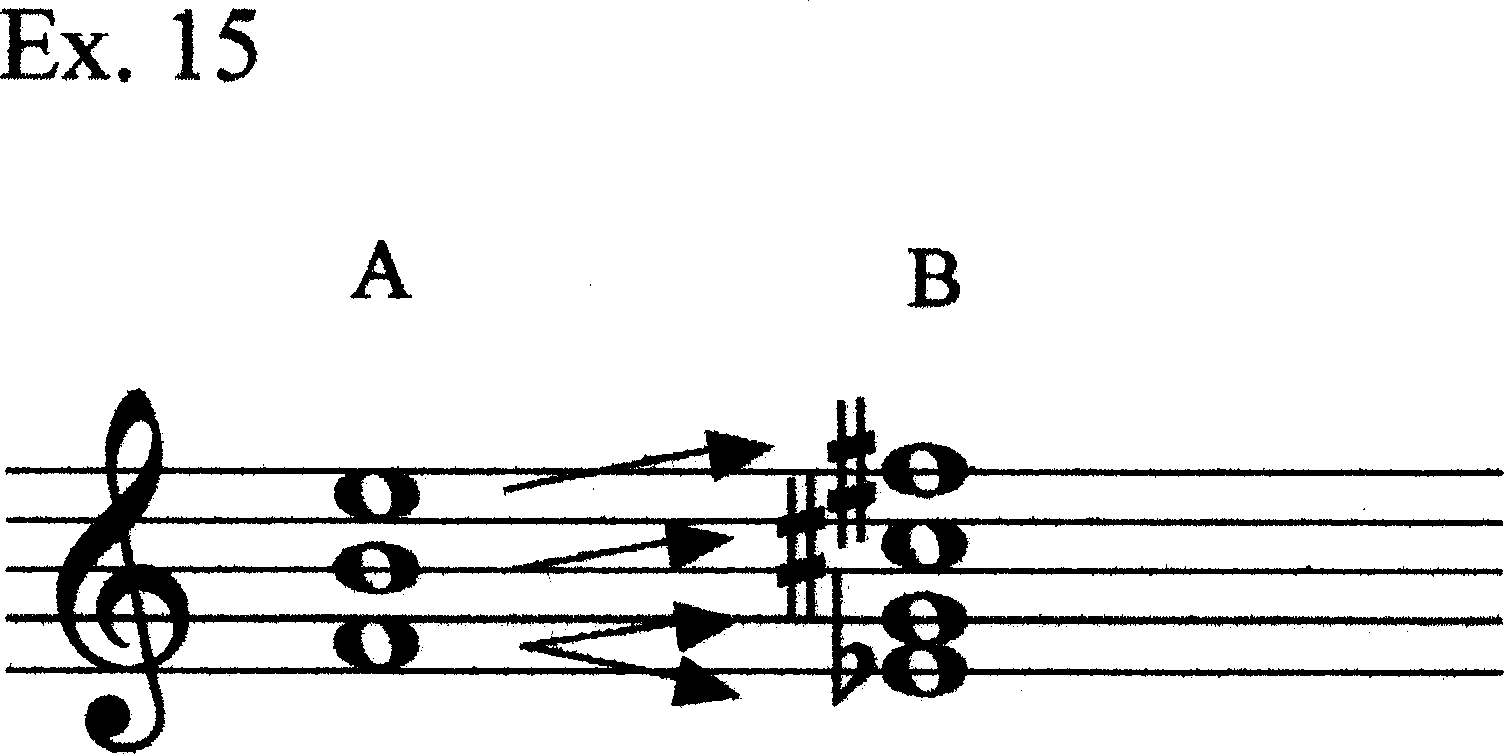
Additionally, there is the problem of what to do with the Eb4 that is the initial pitch of Motive T. The question is: Does the Eb4 belong to the same register as the F4 (Register IV), and thus to the same voice-leading strand, or does it represent Register III? If it is part of Register IV, we would need to invoke a splitting from F4, as illustrated in Ex. 15. If it is part of Register III, then it has no immediate origin; it is the first instantiation of that register. I, myself, incline to the latter view. First, we have heard F4 move up to G4, a motion reinforced by B4 moving up to C#5. Second, we recognize the Eb4 as the lowest note heard thus far. Third, it is quite a bit lower than the notes surrounding it (C#5 and E5). The C#5 is especially significant here. This interval -10 from C#5 to Eb4 implies a registral leap of two strands; adjacent strands have been separated by pitch intervals of 5 or 6 to this point. We might, therefore, consider thinking about Chord B as a four-note sonority, of which the T₂(A) is a trichord subset. [For current purposes, we will focus on the trichord version of Chord B as its essential version.]

Measures 1–9 introduce most of the material for the piece and demonstrate the feasibiltity of tracing harmonies in Alarme. They also contain relatively crisp motivic boundaries and clearly articulated time-spans. We will now work our way through the remainder of the piece. Among other things, we will find that motivic and time-span boundaries are not always as obvious as in the opening bars. The divisions I have made for discussing the piece should not necessarily be interpreted as time-spans usable for a grouping analysis. Here, again, we have to question hierarchical frameworks. My perception of Alarme is that Hermanson often works to thwart our ability to segment the piece in crisp chunks; instead, he wants us to focus on forming associational networks, seeing connections between small ideas and larger patterns of ideas.

b. Measures 10–15.1 (Long melody; Chords A and B again)

This passage can be considered a continuation of the first large section of the piece (that is, the first section might be said to go through m. 15.1, rather than ending at m. 9). Measures 10–15.1 constitute a longer, non-iconic melody built mostly from oscillating figures. Measures 10–12 prolong the F4–B4 dyad. The Eb4–A4 at m. 11.4 is the result of two lower neighbors. Here, the prolongational principle combines simple extension (through repetition) and “away-back” motion. The dyad implies Chord A, even though E5 is not present in this passage. [The issue of incomplete sonorities in atonal harmony will be discussed later.] In mm. 13–14, F4–B4 is replaced by G4–C#5 (again T₊₂ motion); the F#5 that begins at m. 14.4 completes Chord B. [The progression to Chord B again helps us hear mm. 10–12 as implying Chord A (though it is incomplete).]

c. Measures 15.2–18 (Opening sequence; Chord A)

In this passage, we have a variation of the opening six bars. We have Motive S (transposed so that B4 and Bb5 are emphasized), an oscillation of E5 and F4, and a single F4 that represents the steady-state F4 from the opening. In other words, mm. 1–6 encompass a pattern of motives (scream/oscillation/steady-state) that is re-presented in mm. 15–18 in varied (and much condensed form). Probably the most controversial analytic point to this point is the use of this single F4 to stand for a steady-state motive; the restated pattern of motivic sequencing is determinative here. This restatement of Motive S/oscillation/steady-state (the latter two within Chord A) helps articulate the beginning of a new section.

Harmonically, we are still basically working with Chord A. In our analysis of the beginning of the piece, the Motive S was harmonically unconnected to the oscillation/steady-state pitches that follow (and constitute Chord A). If we use the analogous pitches here, we have only E5 and F4, a dyad subset of Chord A. The pitch-level of Motive S here, however, indirectly reinforces Chord A’s role, by emphasizing B4. Bb5 introduces Register VII for the first time. [Register VII is activated only by this note and in this motivic context.]

d. Measures 18.2–25.1 (Chord C)

Measure 18 begins a passage of divergence from Chord A and Chord B. It does so subtly. At first the F#5 invokes Chord B, but then it is embellished with C5, a previously unheard pitch. There have been many int. 6s so far, of course; the tritone is a basic part of the piece. We have heard the B–F tritone (Chord A), the C#–G tritone (Chord B), and (briefly) the A–Eb tritone (as an embellishment of B–F in m. 11). Together, these make a complete whole-tone scale (Whole Tone 1). The F#–C tritone, of course, belongs to the other whole-tone collection (Whole Tone 0), and, thus, represents a fairly significant harmonic departure. [This seems true even though Chords A and B are not whole-tone chords. What is noticeable is the int. 2 voice-leading used exclusively to this point; C5 breaks this pattern.] This embellished F#5, however, has little harmonic connection to what follows. On the surface it most closely resembles the embellished C#5 in mm. 7–8 (Ex. 16). This C#5 is also (of course) part of Chord B. Therefore, the assertion is that F#5 here alludes to Chord B, but the C5 grace note foreshadows the upcoming C4.

The next event is a steady-state siren icon on C4 (the lowest pitch heard to this point, and a representative of Register III). In m. 20, this C4 is embellished with a grace note B4. Measures 21.3–25.1 contain only B4 and F5 (B first as an embellished steady-state motive, then B4–F5 as an oscillating siren). These three pitches, C4, B4, and F5 form a new sonority, Chord C (Ex. 17). Obviously, this sonority is very closely related to Chord A. In pc-space, it has a common tritone. In p-space, the chords are connected by intervals 6 and 11; in Chord A, 6 and 11 are the intervals measured from the bass, whereas in Chord C they are registrally adjacent (Ex. 18).[8] This p-space connection is Jonathan Bernard’s (1987) unfolding (Unfolding 2 of the basic form [5][6]), a special case of Robert Morris’s (1995) FOLDSIM).

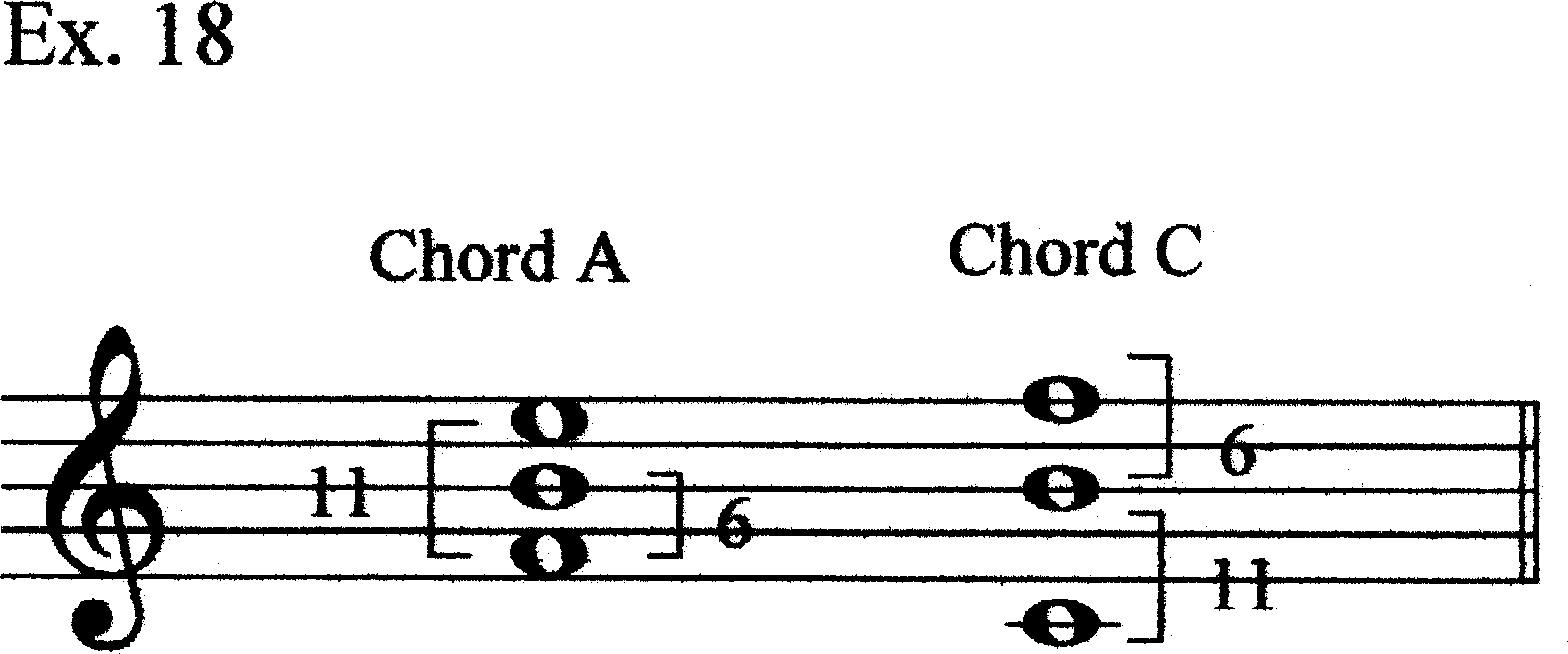
e. Measures 25.3–27 (Chord D)

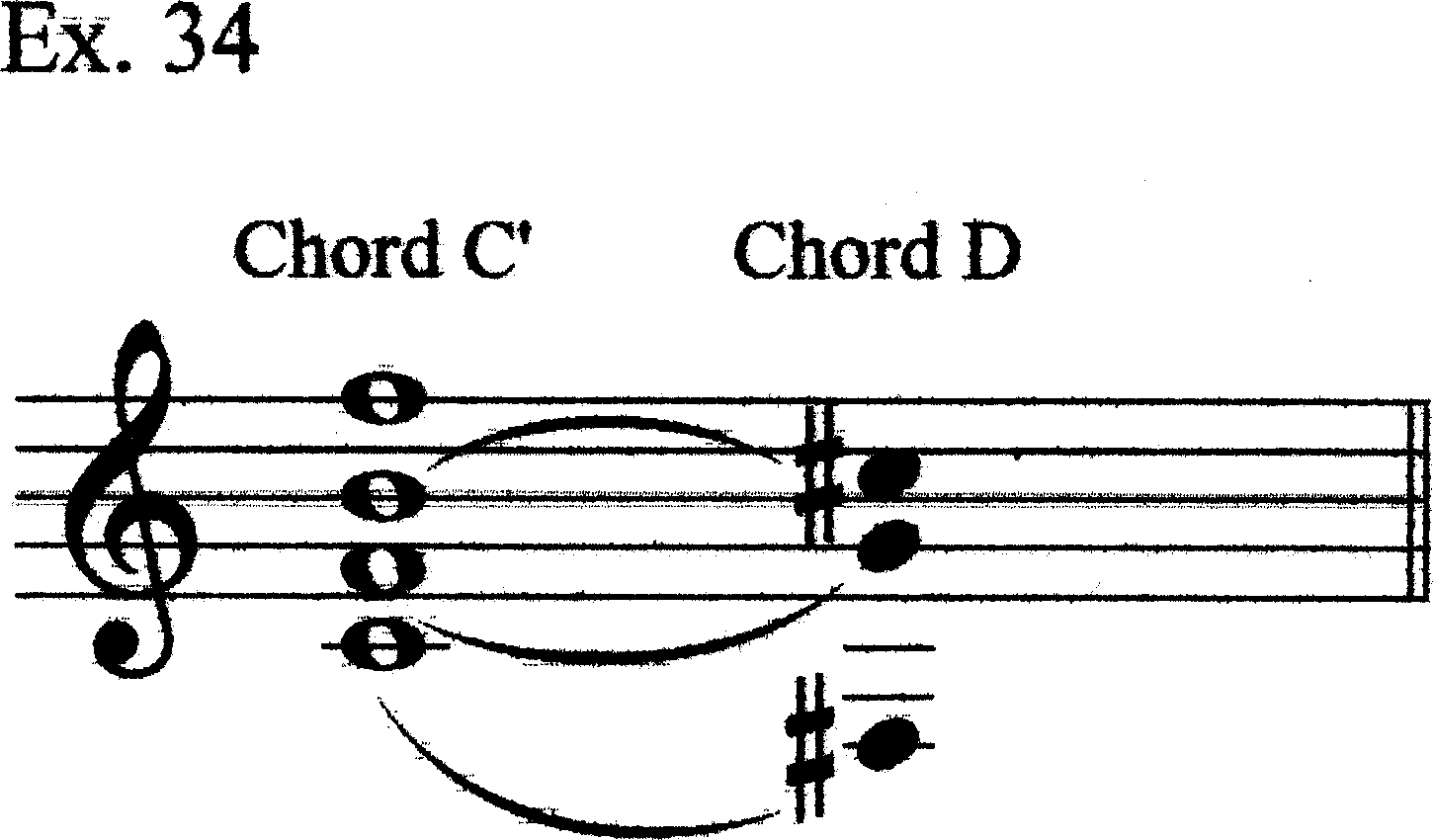
Here is another arpeggiation, C#5, G4, and F#3, consisting of: 1) an embellished singleton; and 2) a steady-state G4/oscillating G4–F#3. The C#5–G4 reacquaints us with the tritone of Chord B (same pitches), whereas the F#3 invokes Register II for the first time. This chord, Chord D, is similar to Chord C, except the lower interval is 13 instead of 11. Obviously, invoking interval classes is tempting here (Ex. 19). Straus would show a voice-leading connection like Ex. 19b, which looks elegant, until one moves back into p-space (where all musical events happen) and one realizes that one has to have three axes-of-symmetry (involving two pcs; Ex. 19c). A dual transformation showing the downward transposition of all voices (and the tritone retained in the top voices) might be more convincing (Ex. 19d).

But neither of these analyses directly takes into account the division of the spectrum into registral space. F5 (the highest note of Chord C) and C#5 (the highest note of Chord D) belong to different voice-leading strands, a point made evident by Hermanson through the grace note B4 embellishing the C#5 in m. 25. The C#5 is connected via T₂ to the B4 from the previous harmony, just as C#5 has been consistently throughout the piece (Ex. 20). Indeed, this register (Register V) is the only one to be represented in both Chords C and D. Neither of the above analyses makes the B–C# connection.

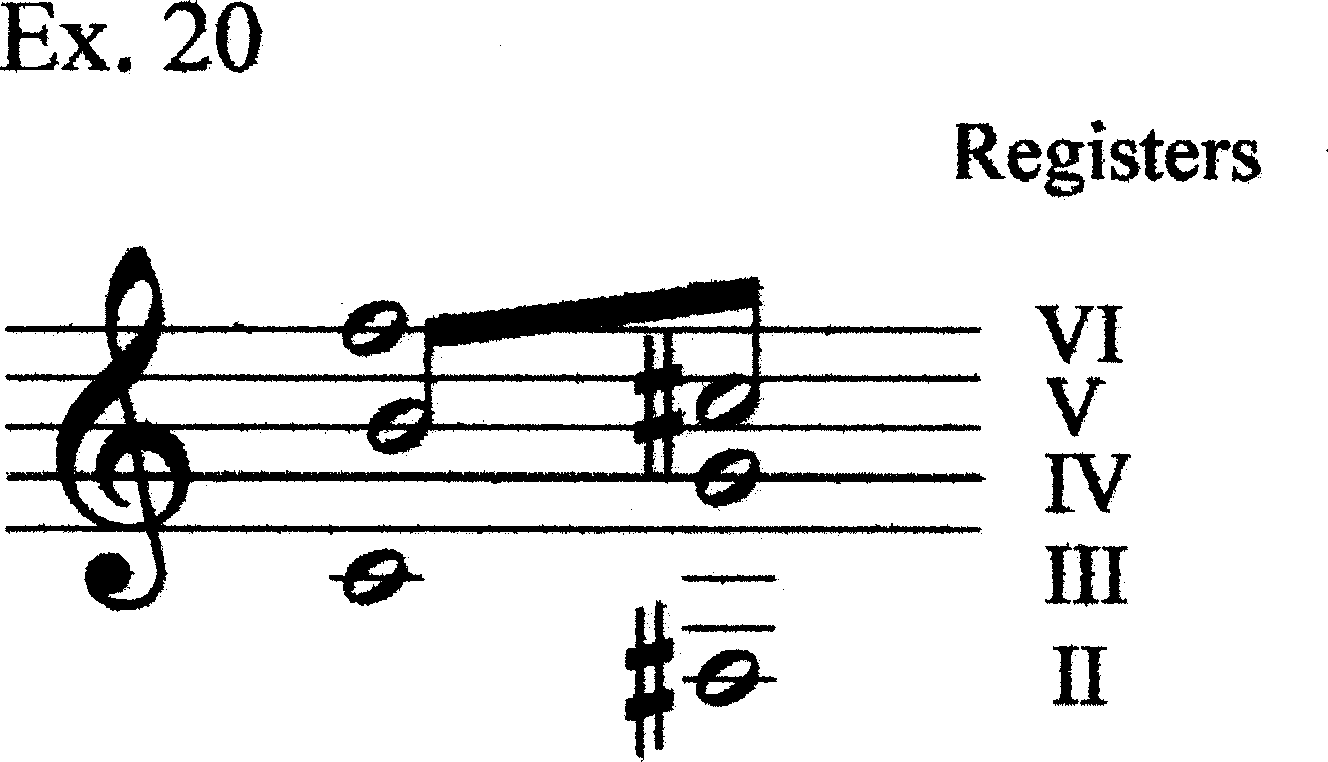
f. mm. 28.1–31.2 (Chord E)

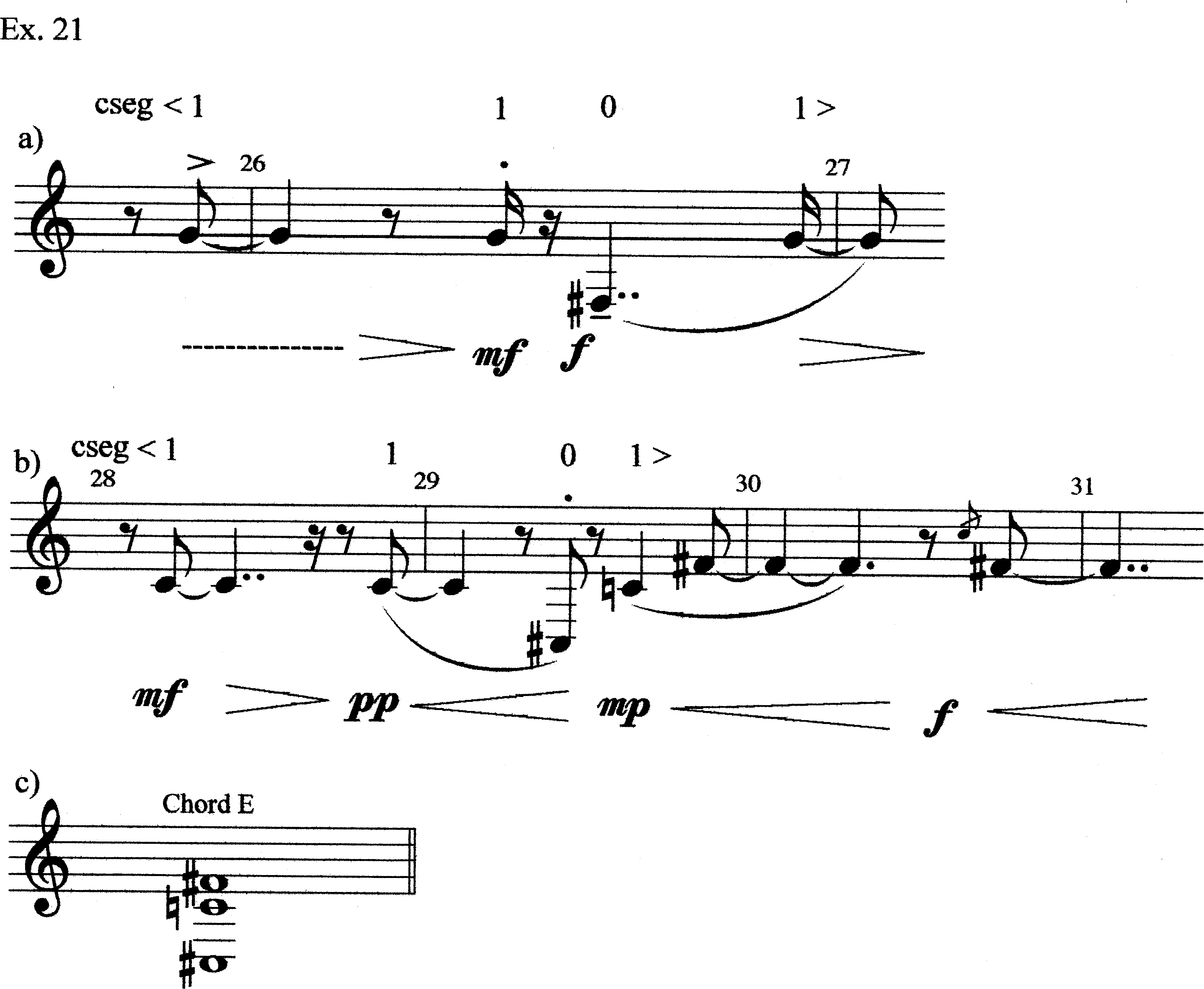
Measures 28.1–31.2 (which are related motivically to mm. 25.4–27.1; Ex. 21) comprise a third chord, Chord E, similar to Chords C and D. Indeed, it is an exact transposition of Chord C, at T_-11. Within the context of Chord E, we must also account for the C5. This, again, is an opportunity for invoking pc-space. We can easily perceive C5 as an inner voice being projected above the soprano.

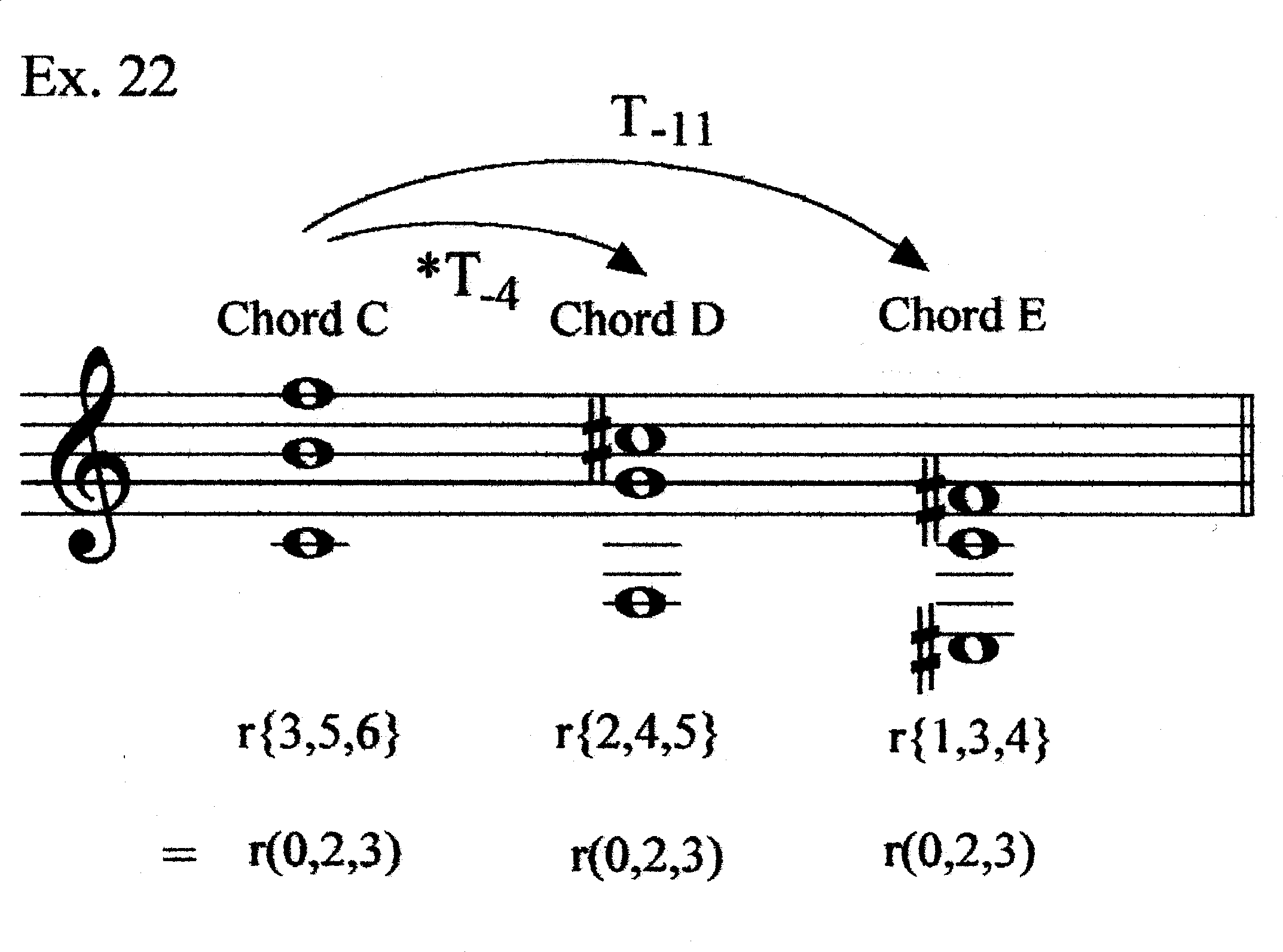
Thus, we have an extended passage, mm. 19.1–31.2, of arpeggiation. The passage uses three chords, each of which has an r-space set of r(023); this means that three registers are represented, with a gap of one missing register between the lower two (Ex. 22). [Chords A and B have r-space sets r(012), utilizing three adjacent registers.] The first and third chords of the passage (Chords C and E) are transpositions of one another, while the second (Chord D) is a near-transposition.[9] Furthermore, these sonorities are clearly related to Chords A and B, which form the harmonic basis of mm. 1–18.

A further word is in order concerning these chords. The Chords C and D have WT-1 tritones, B–F and C#–G, respectively; in this respect, they recapitulate important connections with Chords A and B. Chord E, however, has a WT-0 tritone (C–F#), “anticipated” in m. 18. Therefore, m. 18, (which seems strange when it appears) can be seen as foreshadowing Chord E.

g. Measures 31.3–37.2 (Chord F?; E4–C#5 oscillation)

This is a peculiar passage. It begins with an iconic oscillation of F5 and B4 in mm. 31.3–34.2 (interrupted by an F#4 singleton in mm. 33). This passage is, of course, directly related to mm. 23.4–25.1. This tritone returns us to Chord C (even though C4 is not presented this time); the intruding F# singleton relates back to the Chord E of mm. 28–31.2. Alternatively, however, it would be possible to view mm. 31.3–34.2 as a single sonority (Chord F; Ex. 23a). This chord is clearly relatable to Chord A. This can be seen through a single transformation (I₁₀), a dual transformation (T₀ and T₁) or through positively isographic K-nets; Ex. 23b–d). There are three aspects of the passage that make me consider the F–B dyad and the F# singleton as belonging to separate chords. First, the iconic siren in mm. 31.3–32 was presented in mm. 23.4–25.1 as part of Chord C; the return of the passage, thus, reinvokes the original harmony. Second, F#4 (as part of Chord E) immediately preceded this second F5–B4 siren; the return to F# 4 reinvokes Chord E. Third, the B4–F5 alternation reappears immediately after this F#4; by itself, this would not necessarily imply away-back motion, but the singleton F#4 is dynamically “marked” (sub f, as opposed to the ff F–B). The change in dynamic marks F#4’s intrusion.[10] However, we will soon see how invoking Chord F could help clarify a local voice-leading motion.

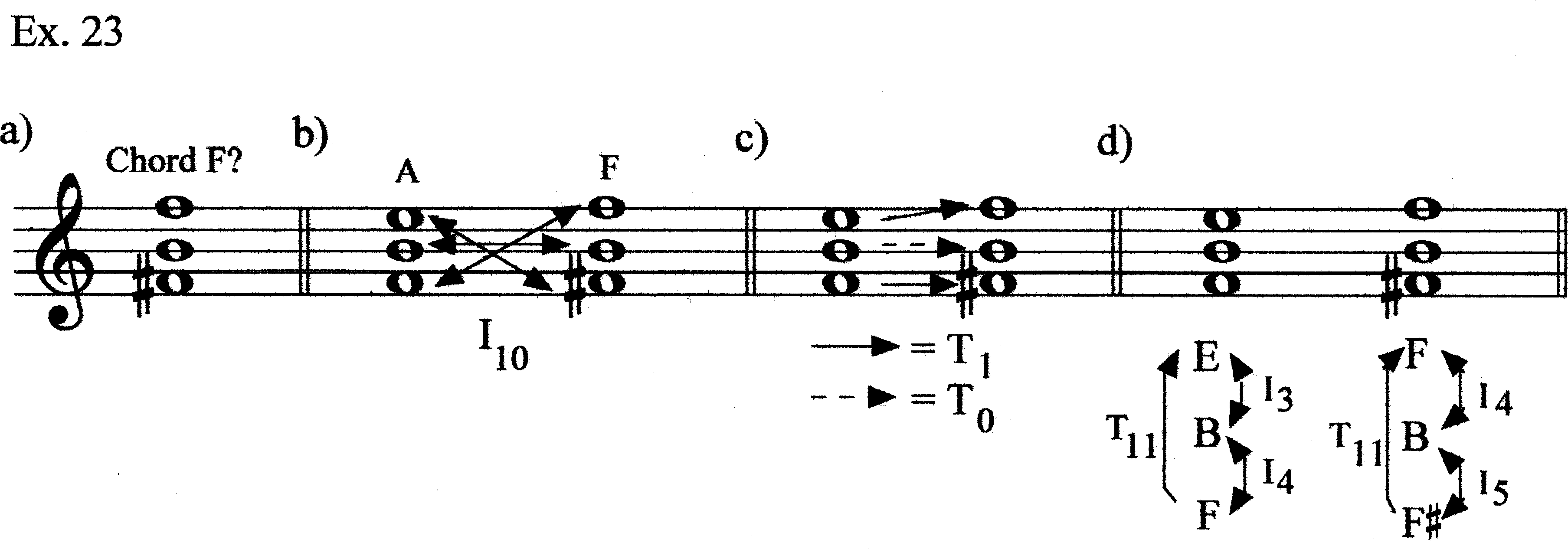
Measures 34.3–35 present an oscillation motion with E4 and C#5. The oscillation is mostly regular (like the iconic oscillations), but the penultimate note is shorter. This is the first time an interval 9 has been presented. The E4 belongs to the same register as F#4 and the C#5 belongs to the same register as B4. Indeed, we have heard B4–C#5 many times in the piece. But a difficulty is presented: E4 and C#5 clearly belong to the same harmony, but their int. 2 predecessors would belong to different harmonies (F#4 from Chord E, B from Chord C). This might be an argument for the idea of a Chord F being a “real” sonority, since it would provide interval-2 precedents for both E4 and C#5 (Ex. 24). We will find that this int. 9 is always surrounded by the B4–F5 tritone, and so is intimately associated with it (and can be seen as the “away” in an away/back motion). [11]

h. Measures 37.2–46 (Varied restatement of mm. 1–18)

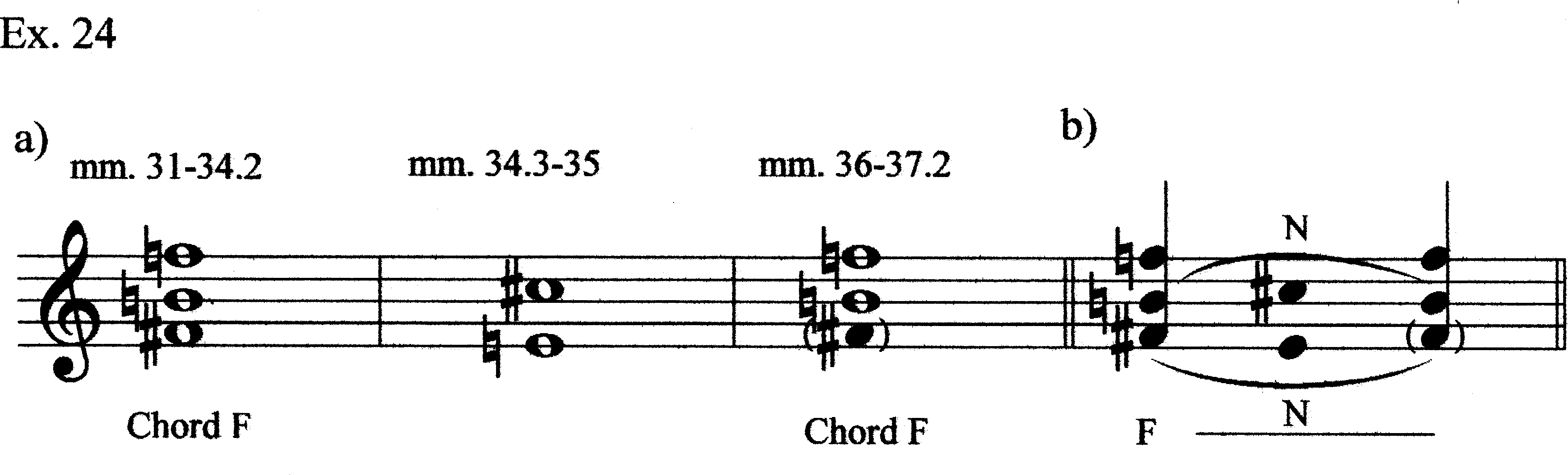
Measures 37.2–41.4 comprise a third rotation of the material of mm. 1–6.3. We have Motive S, a truncated oscillation (E5–F4, as in the second rotation at mm. 15.4–17.1, but having only three notes, and here not all of equal length), then a steady-state on F4 (four statements of eleven sixteenth-notes’ value, separated by one sixteenth rest each time, just as in the beginning). Measures 42.3–44 are an almost exact restatement of mm. 10.2–12.2, with the second half of the melody transposed up two semitones (Ex. 25). Finally, mm. 45–46 present Motive T, altered to end on E5 (rather than F#5), and, therefore, within the Chord A region.

—

i. Measures 47.1–53.1 (Varied restatements; Chords C and B)

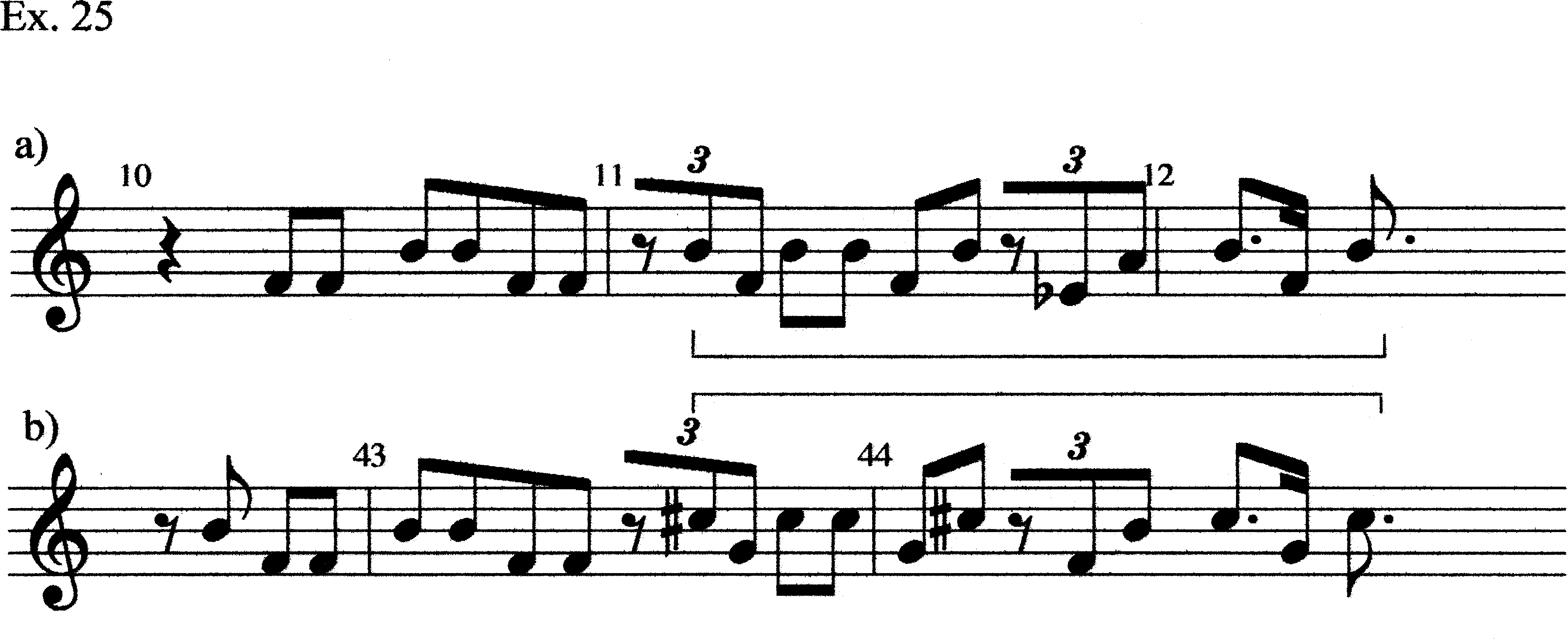
Measure 47.1, by again using F5, signals a change of harmony from Chord A. The F5 is followed by the E4–C#5 oscillation (a shortened version, with its beginning clipped). In mm. 48–49.2, the F5–B4 tritone recurs. Thus, mm. 47–49.2 constitute a shortened restatement of mm. 33.4–37.2 (Ex. 26). In mm. 49.3–51 we have two tritones, Eb4–A and B4–F5 presented; obviously, the B4–F5 tritone implies Chord C. [This passage will be dicussed in more detail below.] In mm. 52–53.1 we have the B chord (see mm. 13.2–15.1).

—

j. Measures 53.2–59.1 (Chord C)

In mm. 53.2–56.2 we have a steady-state icon on C3, the lowest note presented so far. This, of course, is the same icon as appeared in mm. 3.3–6.3. In mm. 56.3–59.1, we have the B4–F5 tritone alternating with the E4–C#5 int. 9, resembling mm. 33.4–37.2 and mm. 47–49.2 (Ex. 27). How, then, does the C3 fit in? One possibility is to link it with the B4–F5 that follows. In this reading, the chord is an altered version of Chord C, with C4 being replaced by C3. The identification of the following passage (mm. 56.3–59.1) as a restatement of an earlier passage may be taken as reinforcing the connection to Chord C (compare mm. 53.2–57.3 with mm. 19.1–25.1 (the harmony that is the background for mm. 33.4–37.2)). Although pc-space has to be invoked, it does not involve a registral re-ordering. Further, Chord C’s C4 was already relatively removed from its other notes (B4–F5); there was a registral gap (there was no note from Register IV), whereas previous chords had employed three notes from adjacent registers. In this case, that gap is extended by two more registers.[12]

k. Measures 59.1–69 (Chord A)

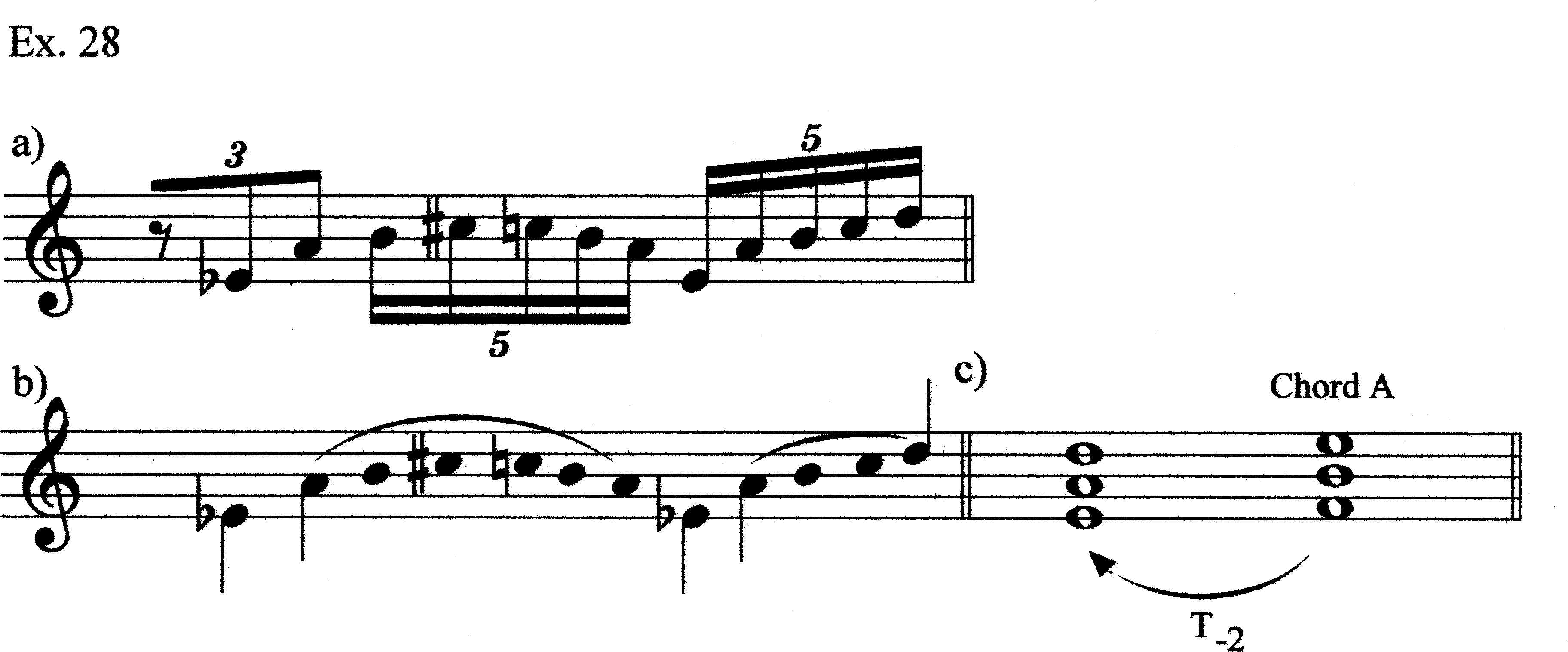
The B4 at m. 59.1 acts as a pivot pitch from Chord C back to Chord A; after the B4, we have an oscillation on E5 and F4 through m. 61.1. In the remainder of m. 61 we get our only “flourish” of the piece. I see the harmony underlying this passage as that shown in Ex. 28, a T_-2 transposition of Chord A. This is followed by Motive T (first incomplete, then complete, then incomplete again). The remainder of the piece is from Chord A, with the exception of the F#5 interruption in mm. 66.4–67. This seems analogous to the F#4 interruption in m. 33.1–3.

3.2 Further Reduction and Prolongation

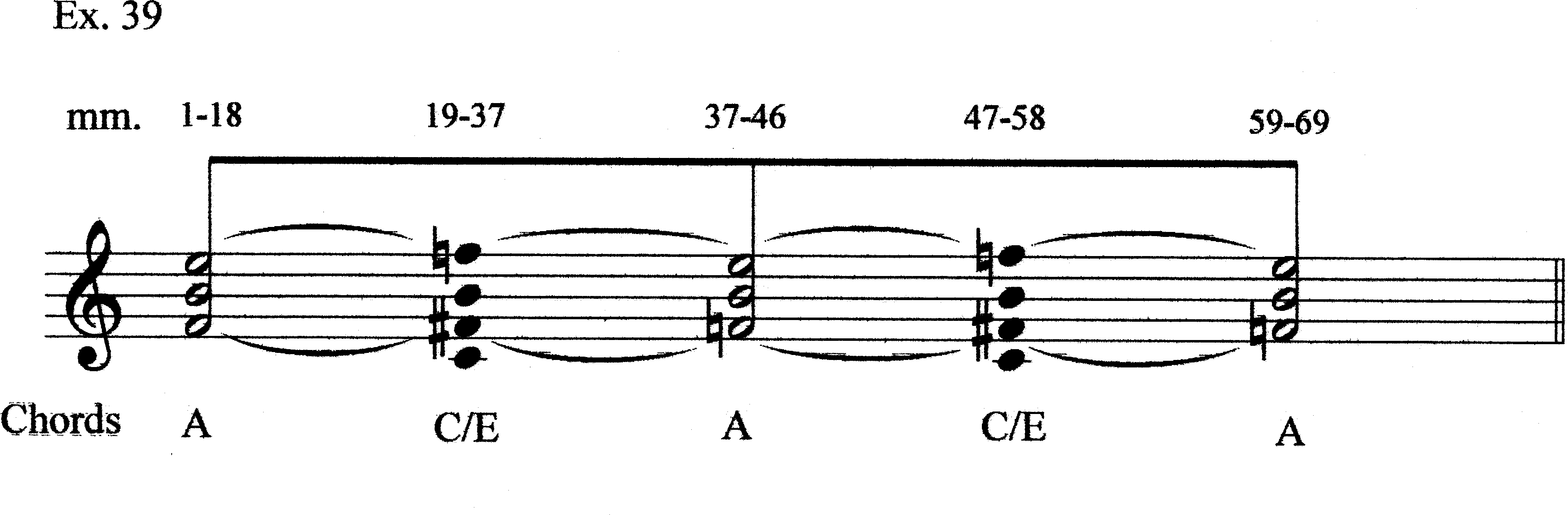
3.2.1 Chord Regions and Prolongation

Our chord motions are summarized in Ex. 29; omitted or “additional” tones are shown with filled noteheads. The question now is how these chords can be thought of in prolongational terms. In the opening section, Chords A and B alternate. We might see A to B motion as a progression repeated, then started a third time (Ex. 30a); or, we might see Chord A as being prolonged by its T₂-associate, controlling the span of mm. 1–18.1 (Ex. 30b). Measures 19–37.2 mostly involve three chords similar to one another, but different than the ones of the preceding section. Chord C and E are transpositionally related; Chord D is a near-transposition. All involve rsets of r(023) (differentiating this section from mm. 1–18). One of the ways that this section is problematic from a prolongational point of view is that the three chords involve different sets of registers (unlike Chords A and B, which involved the same registers). Since introducing a new register would imply arpeggiation within a chord, we may have to review our chord boundaries to see a sonority that operates on a larger scale.

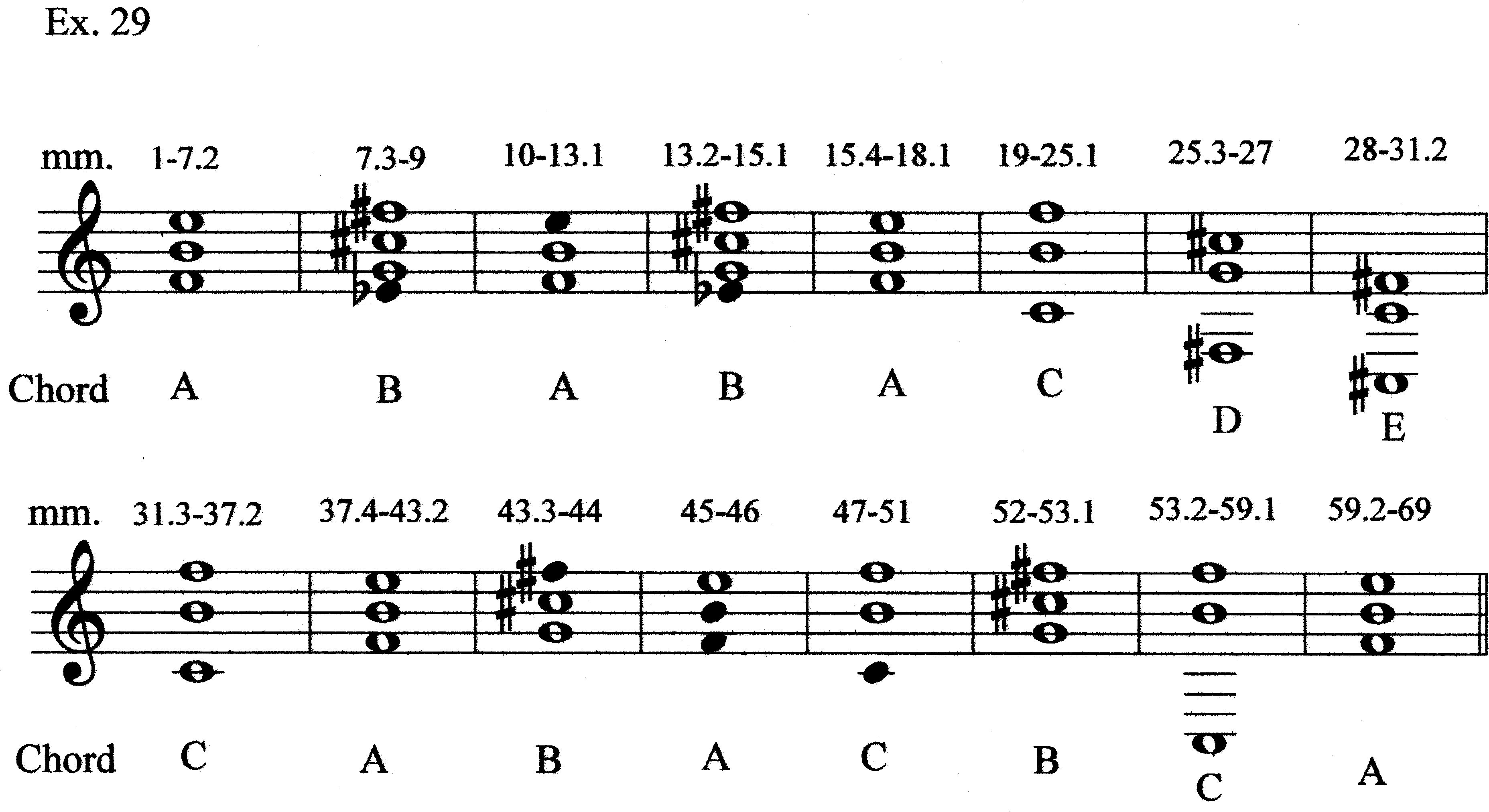
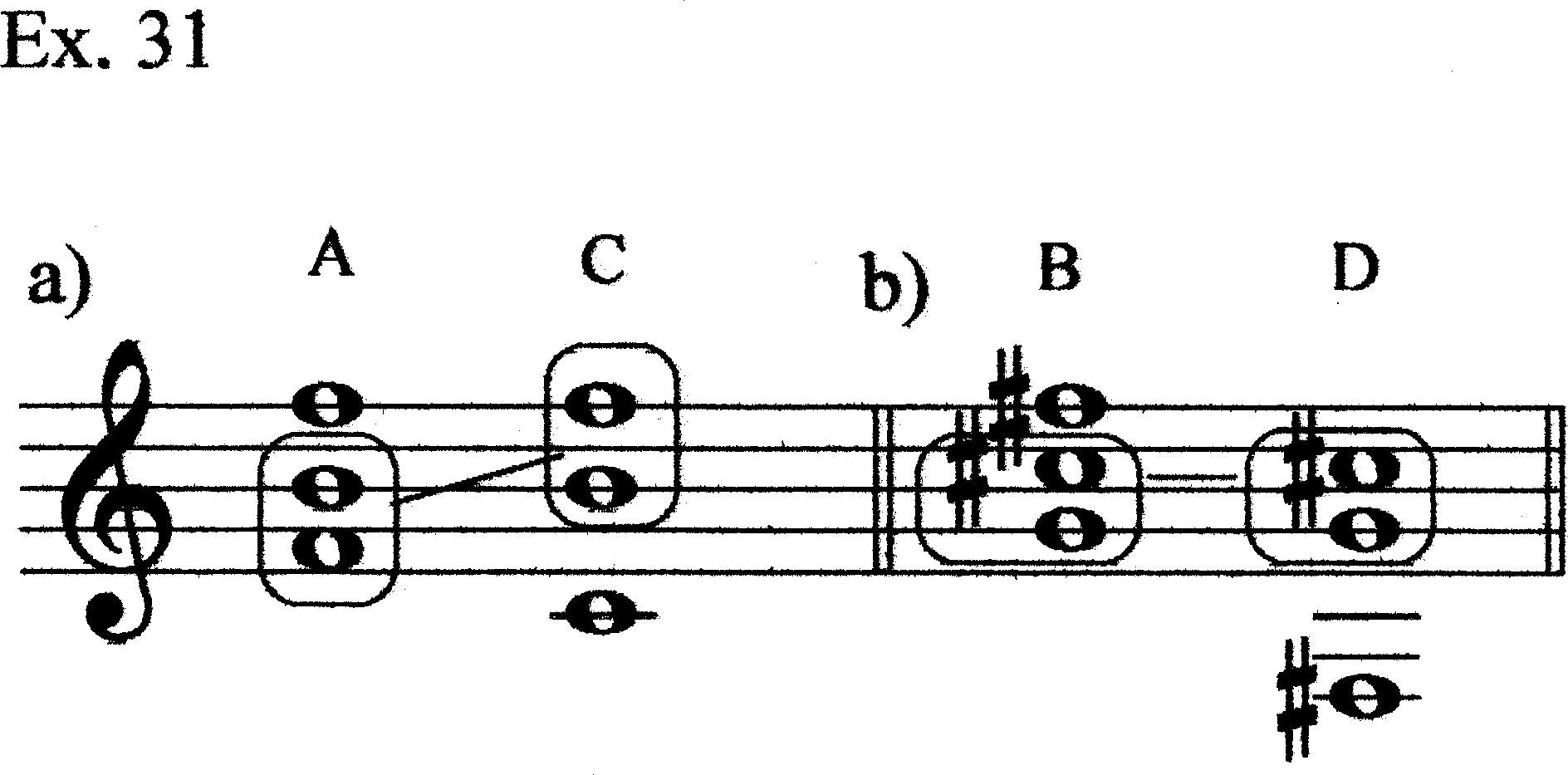
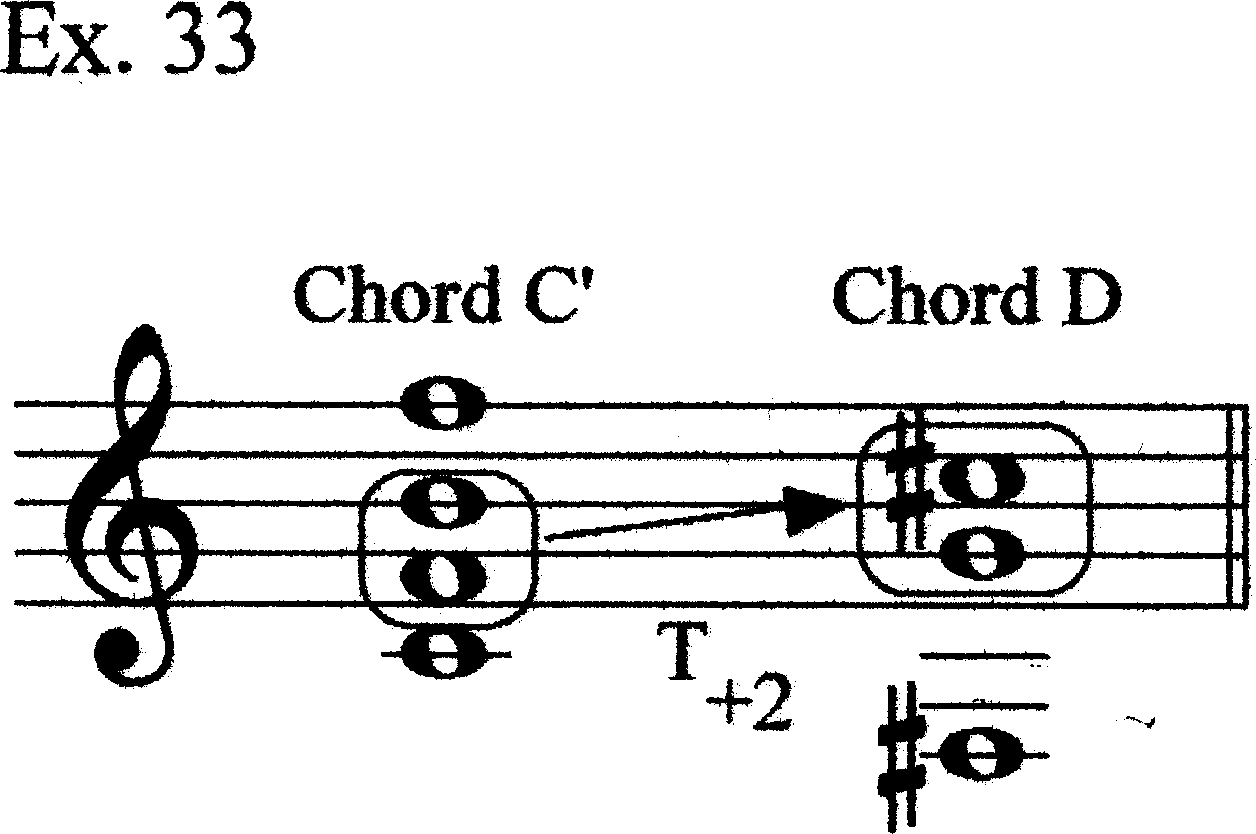
Although Chords C and D (and E) have different spacings than Chords A and B, they nevertheless share some common elements. Example 31 shows how Chords C and D are related to Chords A and B, respectively. Building on the idea of B’s subordination to A, we can hypothesize a path through the harmonies of mm. 18–37.1. First, E5 of Chord A moves to F5 of Chord C. We might think of F5 as being a projection of F4, but it is not necessary to invoke that idea yet (if at all). We could, instead, think of E5 as moving to F5, with F4 still present in Register IV (Ex. 32). We then add C4 to the bottom of the sonority giving us Chord C’ as an expanded version of Chord C. This allows us to view the C#5 and G4 of Chord D as again involving T₊₂ relations from F4–B4 (Ex. 33). We can, thus, by relying on Hermanson’s use so far of C#–G to prolong B–F, think of Chord D as prolonging Chord C. The lowest note, F#3 is a new one; our “bass” voice is moving down (Ex. 34). [This assertion creates a problem we will discuss shortly.] Chord E has the C4–F#4 tritone; C4 is already in Chord C, while F#4 is F4 moving up a semitone (just as E5 moved to F5 in going from Chord A to Chord C). We can, therefore, fuse Chords C and E into a single larger sonority having four main notes in Registers III, IV, V, and VI, with a coloristic added note below in Register I (C#3; Ex. 35). We have already explicitly put such a note under Chord B (Eb4) and implicitly in Chord D (F#3), by focusing our Chord D attention on the C#5–G4 tritone’s T₂-relation to B4 and F4 of Chord C’. The motion from Chord A to Chord C/E takes place in two phases: 1) E5–F5, with C4 added; and 2) F4–F#4, with C#3 added (Ex. 36).

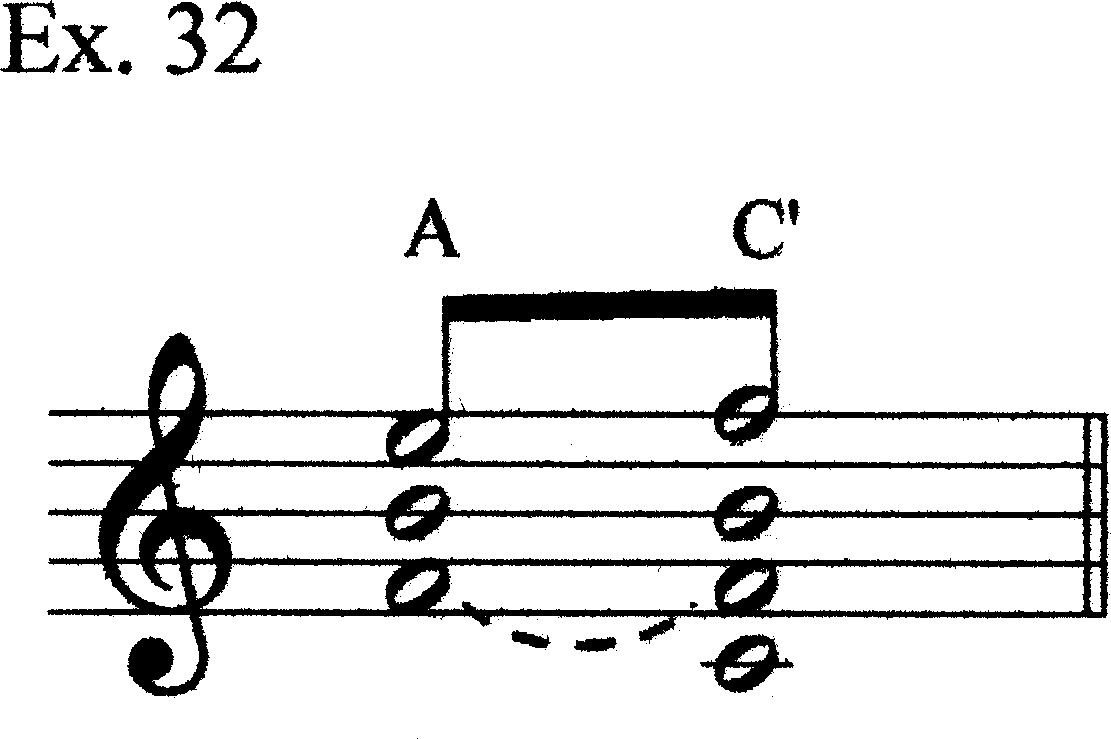
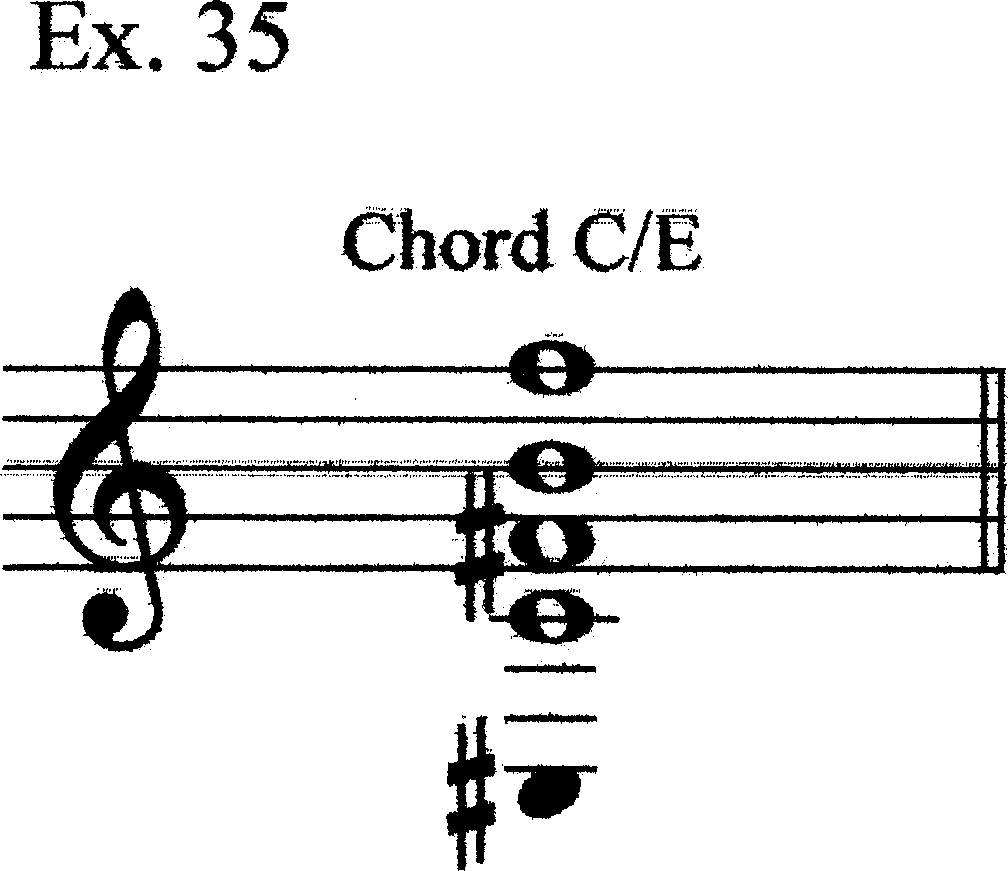
This invocation of a leaping bass is obviously tempting for several reasons. First, the lowest notes in chords generally garner special attention, and in tonal music, the bass line is astonishingly important. Second, bass lines in tonal music are different from upper voices; whereas skips in upper registers almost always imply motion to a different voice, bass voices almost by definition leap. However, we would do well to resist the temptation to having a leaping bass in the case of Alarme, if for no other reason than to have a consistent notion of r-space. As formulated in the analysis, all registers operate in the same way in principle (some registers are largely “neglected” in the piece, and so it is not immediately obvious that they are being treated identically to more active registers).

The remainder of the piece (mm. 37.2–69) is reduced in Ex. 37. Perhaps the most problematic spot here is in mm. 49.3–51, where the Eb4 and A4 tritone is paired with the B4–F5 tritone. We have encountered the Eb4–A4 tritone earlier, and analyzed it as constituting lower neighbor tones to F4–B4. That Eb–A is imediately followed by F–B reinforces the pc-relation and, by extension, the connection between Chords A and C (with their common F–B tritone). It might even lead us to hear F5 as a projection of F4 up the octave (and, by extension, the unfolding operation).

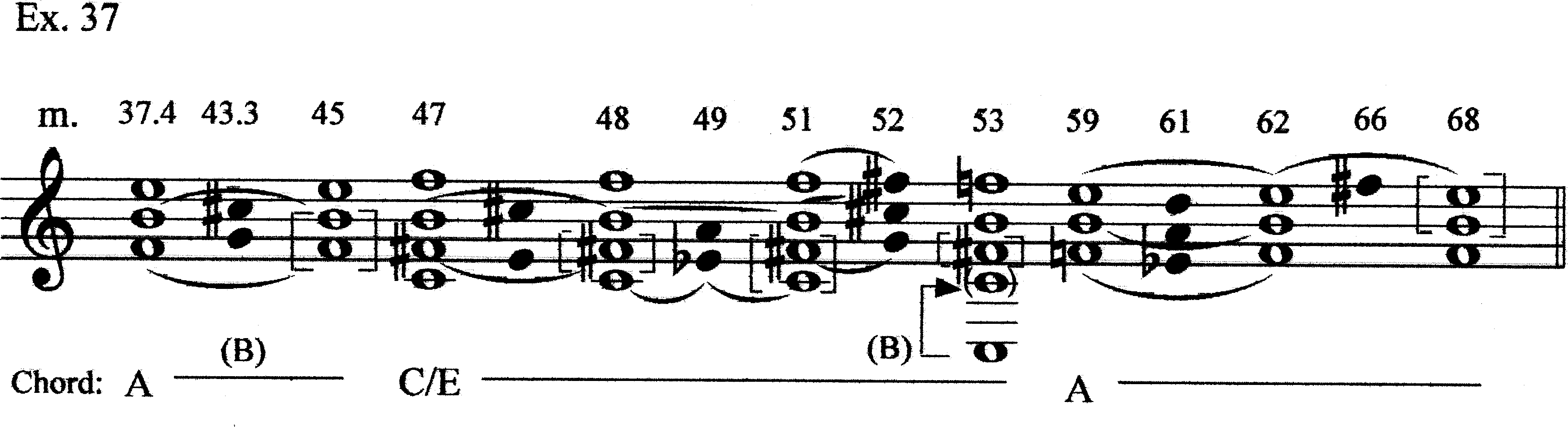
However, we have endeavored to limit pc-relations as much as possible, and we may have a less immediate, but still plausible alternative expanation. The B4–F5 tritone implies Chord C, which has a C4 from Register III beneath it. Eb4 has been invoked as a member of Register IV (as a lower neighbor to F4), but also as a member of Register III in Chord B. If this Eb4 is a representative of Register III, it then acts as an upper neighbor (neighboring 3rd) to the implied C4 of Chord C (Ex. 38). Of course, in tonal music implied resolutions occur frequently, especially when the surface number of “voices” in a piece drops (say, in a piano texture when a three-voice texture suddenly becomes a two-voice texture) or in a sequential passage where there are more voices than lines. While this explanation might not be one’s first intuition, it does keep voice motion within registral streams (rather than invoking octave displacements), thus preserving our starting point of using streams as the basis for voices. Example 39 is a deep background for the piece.

4. Conclusion

In this essay, I have explored how within the context of an atonal piece without any simultaneities, chords can be created within the listener’s mind (or, more accurately, how chords can be assembled by the listener). Crucial to this process is the notion of fusion (in Lerdahl’s expanded sense) and the idea of register space. The notion of r-space led us to create associational voices, which could then be traced through harmonic changes. The resulting voice motions can then be used to establish harmonic prolongations governing large stretches of music. 

Obviously, few works involve such a limited intervallic repertoire and such crisply defined registral boundaries as Alarme. While it is fruitful to apply the principles discussed here to Hermanson’s other solo pieces, similar pieces by other composers will likely present more blurred pictures. Nevertheless, it is hoped that this analysis can serve to clarify how voices are constructed and move in atonal repertoires, including Hermanson’s larger works.

Works Cited

Baker, James M. 1983. “Schenkerian Analysis and Post-Tonal Music” in Aspects of Schenkerian Theory ed. David Beach. New Haven: Yale University Press, 153-88.

Bergendal, Göran. 2007. “Liner notes for Åke Hermanson: Alarme.” trans. by Isabel Thomson. CAP 22056.

Bernard, Jonathan. 1987. The Music of Edgard Varése. New Haven: Yale University Press.

Bregman, Albert S. and J. Campbell. 1971. “Primary Auditory Stream Segregation and Percepetion of Order in Rapid Sequences of Tones.” Journal of Experimental Psychology 89: 24-29.

Chapman, Alan. 1981. “Some Intervallic Aspects of Pitch-Class Set Relations.” Journal of Music Theory 25: 275-90.

Forte, Allen. 1955. Contemporary Tone Structures. New York: Teachers College, Columbia University.

Katz, Adele. 1972. Challenge to Musical Tradition. New York: Da Capo Press. First published 1945.

Lerdahl, Fred 1989. “Atonal Prolongational Structures” Contemporary Music Review 4: 65-87.

———. 1997. “Issues in Prolongational Theory: A Response to Larson.” Journal of Music Theory 41: 141-55.

Lerdahl, Fred and Ray Jackendoff. 1983. A Generalized Theory of Tonal Music. Cambridge, MA: The MIT Press.

Morris, Robert D. 1995. “Equivalence and Similarity in Pitch and Their Interaction With PCSet Theory.” Journal of Music Theory 39: 46-91.

Salzer, Felix. 1982. Structural Hearing: Tonal Coherence in Music. New York: Dover Publications. First published 1952.

Straus, Joseph N. 1987. “The Problem of Prolongation in Post-Tonal Music.” Journal of Music Theory 31: 1-22.

———. 1997. “Voice Leading in Atonal Music” in Music Theory in Concept and Practice, 237-274 eds. James Baker, David Beach, and Jonathan Bernard. Rochester, NY: University of Rochester Press.

Travis, Roy. 1959. “Toward a New Concept of Tonality,” Journal of Music Theory 3:257-84.

———. 1966. “Directed Motion in Schoenberg and Webern,” Perspectives of New Music 4 : 84-89.

Väisälä, Olli. 2004. Prolongation in Early Post-Tonal Music: Analytical Examples and Theoretical Principles. Helsinki: Sibelius Academy.

---

Notes

©Stephen Harper, 2007

STM-Online vol. 10 (2007)
http://musikforskning.se/stmonline/vol_10

Webmaster: webmaster@musikforskning.se

ISSN: 1403-5715